Research Interest
My research explores many-body quantum dynamics in the era of digital quantum computers. The emerging non-equilibrium phases of matter, naturally described by quantum circuits, lack traditional order parameters like magnetization and are instead characterized by quantum information resources. I study how these complexity measures propagate and evolve in many-body systems and how measurements and noise alter and enrich the resulting phases.

Quantum circuits
Quantum circuits are a fundamental tool for exploring the dynamics of quantum systems, providing a flexible and scalable framework to study entanglement, information scrambling, and non-equilibrium phase transitions. Unlike traditional Hamiltonian approaches, which describe static or continuously evolving systems, quantum circuits naturally model discrete-time evolution, making them particularly relevant for quantum computation and simulation. They allow for precise control over quantum operations, enabling the realization of complex quantum states and the investigation of error resilience, measurement-induced phenomena, and novel phases of matter. I am interested in the evolution of quantum resource theories in many-body dynamics described by quantum systems. The aim of these results is to bridge between theoretical quantum many-body physics and practical quantum technologies, offering insights into quantum error correction, complexity theory, and the fundamental limits of quantum information processing. Viceversa, a better knowledge of resource theory enable a more comprehensive understanding of quantum matter, beyond the traditional Landau-Lifshitz paradigm based on order parameters.
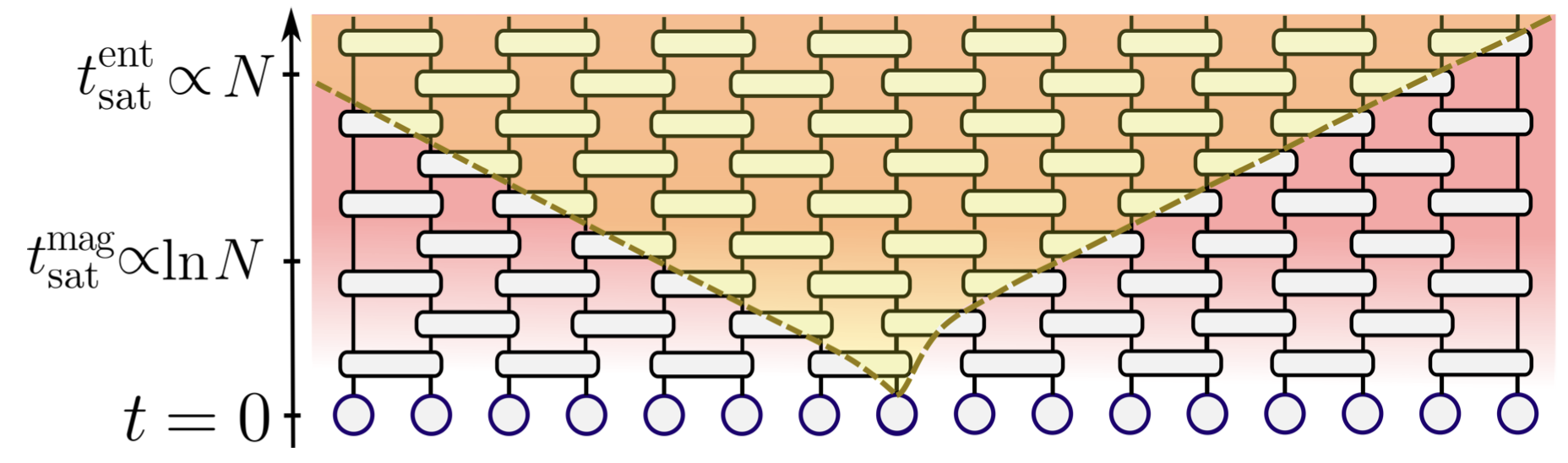
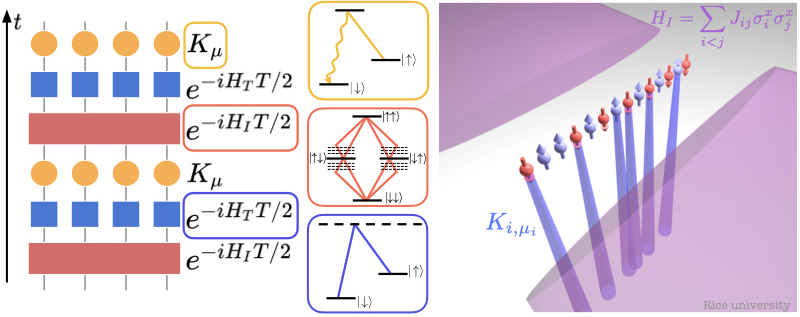
Monitored quantum dynamics
A defining feature of quantum systems is their sensitivity to measurement: monitoring a quantum many-body system fundamentally alters its dynamics, leading to emergent phases that have no classical counterpart. The interplay between unitary evolution, which scrambles information and generates entanglement, and measurements, which localize information and collapse the wavefunction, gives rise to measurement-induced phase transitions. These transitions delineate regimes where quantum information is either robust—enabling error correction—or suppressed, as in the quantum Zeno effect, where frequent measurements constrain the system’s evolution to a lower-dimensional manifold. My research investigates how monitoring shapes quantum many-body dynamics, focusing on its role in quantum information encoding, entanglement structure, and the emergence of new dynamical phases. I explore these phenomena in both random quantum circuits, where measurements compete with unitary gates in discrete time, and fermionic quantum systems, where continuous evolution is punctuated by quantum jumps. These settings provide complementary perspectives: random circuits serve as minimal models for understanding measurement-induced transitions, while fermionic systems allow for exact solutions and quasiparticle descriptions, shedding light on the fundamental mechanisms underlying monitored quantum dynamics.
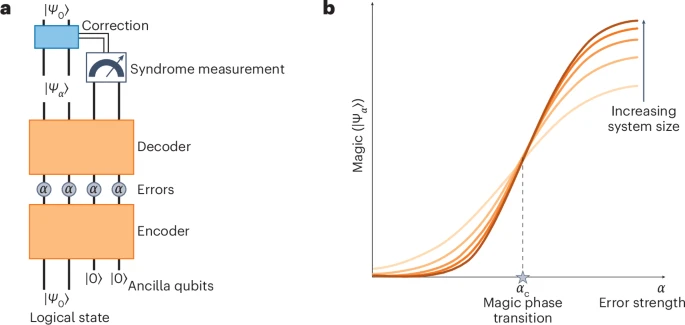
Many-body quantum magic
The concept of magic, or nonstabilizerness, is emerging as a fundamental resource in quantum many-body systems, complementing entanglement in characterizing quantum states and dynamics. Unlike stabilizer states, which can be efficiently simulated classically, states with high magic exhibit computational complexity and underpin universal quantum computation. In the context of quantum circuits, magic propagates dynamically, influencing quantum chaos, error correction, and phase transitions. Recent studies have revealed magic phase transitions, where the amount of nonstabilizerness in a system undergoes sharp changes due to the interplay between unitary evolution, measurements, and noise. Understanding these transitions is crucial for identifying the mechanisms that generate and sustain quantum computational advantage. My research focuses on developing theoretical and numerical tools to quantify magic in many-body systems, analyze its spreading in monitored circuits, and explore how it can be harnessed for robust quantum information processing.